最近看了见识和原则这两本书, 收获很多, 虽然现在因为各种原因还没有打原则这本书看完,其中现在对我感触最深的就是要打造一个自己的算法系统,让自己养成这个习惯,不断的推动自己前进。回顾自己之前的生活,其实在创业之前是目标明确有确定的生活规律或者说是算法;早七晚七,然后从21点开始, 一直完善系统到晚上23点,然后睡觉,早5起床,早七上班。
自从开始创业后,到现在,已经4年了,前一两年因为事情多,杂,逐渐变得没有规律,一直在加班和去加班的路上,一直忙工作上的事情,忽略了生活 和自身的提高,4年里, 没有看什么书, 没有写什么日志,没有什么心得,感觉就是消失的4年,现在回想起来坡为悔恨,现在是时候回归自我。
回归自我先给自己设置一个作息规律先,前一段时间的计划是, 9点上班, 18点忙完工作,然后看一个小时书到19点, 再静坐一些回想总结一下到20点,回家吃饭,执行了一周发现执行不下去了,究其原因,一是下班时间不是固定,有的时候一件事情拖到19点还没有完成,2是家里有小孩子,需要回家照顾,3是20点回家后, 父母等自己吃饭, 吃完饭都快21点了, 这样子下来,晚吃饭又导致自己身体肥胖。
这段时间审视自己的身材,胖了好多,一个人连自己的身材都管不好, 还能管好什么?
计划赶不上变化,但自身算法还是要建立,之前的不适合,先做一个简单修改,后按具体情况逐渐调整完善
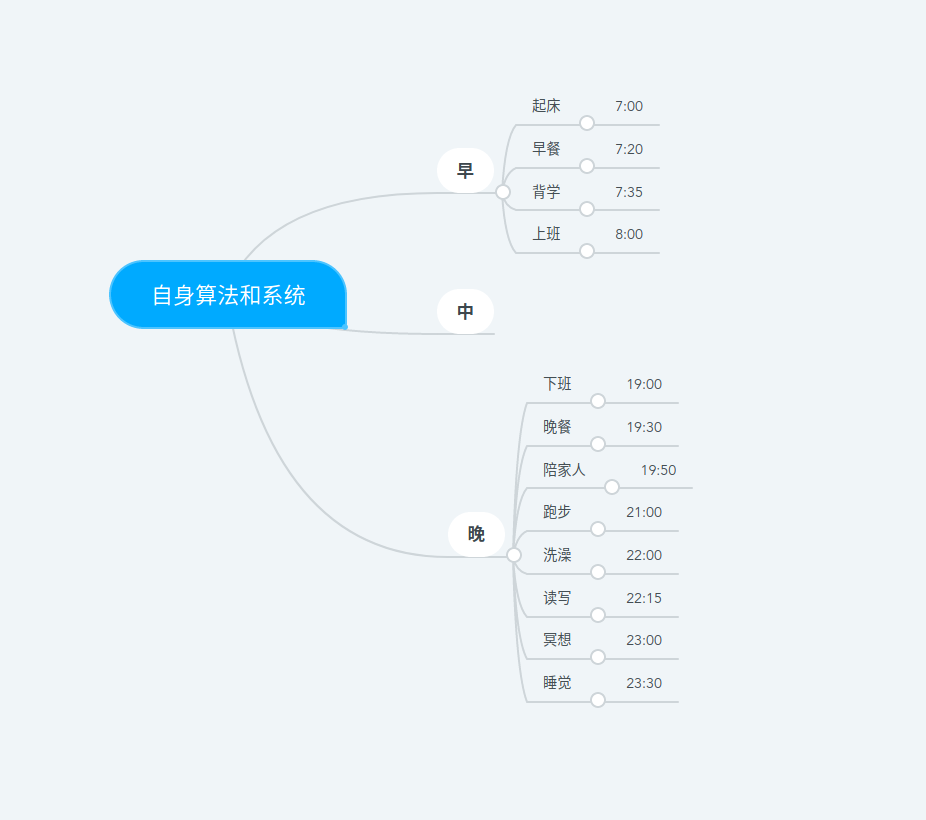
上述算法自2020年06月2号起开始实行, 本次更新时间为2020年06月01号 23:59分